Qual è 'l geomètra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige,
tal era io a quella vista nova:
veder voleva come si convenne
l'imago al cerchio e come vi s'indova;
ma non eran da ciò le proprie penne:
se non che la mia mente fu percossa
da un fulgore in che sua voglia venne.
“Uh, la Divina Commedia”.
“Già. La parte finale dell'ultimo canto del Paradiso, la fine del viaggio”.
“La visione di Dio, vero?”.
“Esatto. Dante arriva davanti a Dio, e cerca di comprendere il mistero della Trinità: gli appaiono tre cerchi, di uguale dimensione ma di colore diverso. Cerca di spiegare quello che ha visto, ma ammette il fatto che le sue parole non sono sufficienti per descrivere tutto. All'interno del secondo cerchio, poi, Dante scorge un'immagine umana”.
“Gesù”.
“Sì. Ed ecco che si affaccia alla sua mente un altro mistero: la coesistenza in un'unica persona della natura umana e di quella divina”.
“Questo è ancora meno comprensibile del precedente”.
“E infatti Dante fa un paragone molto particolare per descrivere l'incapacità della sua mente di comprendere questo mistero”.
“Mi pare che tu ne avessi già parlato”.
“Ah, bene, vedo che hai buona memoria! Sì, il paragone è quello dello studioso di geometria, che cerca di risolvere un problema molto difficile, quello della quadratura del cerchio”.
“A me questa cosa della quadratura del cerchio ha sempre fatto ridere. Mi immagino uno che a suon di martellate cerca di dare forma quadrata a una ruota”.
“Santo cielo. No, non si riferisce esattamente a questo il problema”.
“Lo sospettavo”.
“Ricorderai che i greci avevano delle regole molto precise per lo sviluppo della loro geometria”.
“Ricordo che volevano usare soltanto riga e compasso”.
“Esatto. Riga senza segni, compasso che si richiude dopo aver tracciato un cerchio. Insomma, una geometria senza numeri e poche regole di base”.
“I greci non erano normali”.
“Ti ripeti, sai?”.
“Eh, pazienza. Ma quindi, possiamo usare un compasso ma non riusciamo a quadrare il cerchio. Cosa vuol puoi dire, quadrare il cerchio?”.
“Vuol dire costruire, utilizzando soltanto riga e compasso, un quadrato avente la stessa superficie di un cerchio dato”.
“Fammi capire, bisogna che provi con dei numeri”.
“L'area di un cerchio di raggio r è uguale a πr2”.
“Ok”.
“Quindi devi costruire un quadrato di lato r√π”.
“Bene”.
“Ora, r è solo un fattore di scala, prendila come unità di misura. Il problema è costruire, con riga e compasso, un segmento lungo √π”.
“Sì, giusto”.
“Se riesci a disegnare un segmento, riesci a disegnare anche la sua radice quadrata, e viceversa”.
“Ah sì?”.
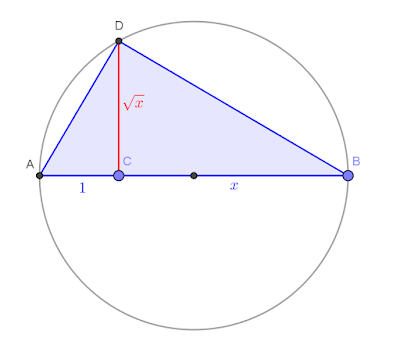
“Sì, grazie ad esempio al secondo teorema di Euclide. Dato un triangolo rettangolo, il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per dimensioni le due proiezioni dei cateti sull'ipotenusa”.
“Eh?”.
“Guarda questa figura:”.
“Ok”.
“Il quadrato di lato CD ha la stessa area del rettangolo di lati AC e CB”.
“Cioè x”.
“Esatto. E quindi se un quadrato ha area x, il suo lato sarà…”.
“Radice di x! Bene, ho capito”.
“Quindi costruire √π o costruire π è la stessa cosa: se sai costruire uno dei due sai costruire anche l'altro”.
“Va bene, quindi il problema della quadratura del cerchio si traduce nella costruzione di un segmento lungo pi greco”.
“Proprio così. Ora, con riga e compasso non si riesce a costruire proprio tutto quello che si vuole”.
“Ricordo”.
“Esiste una categoria di numeri costruibili”.
“Certo, esistono categorie per tutto”.
“Quella dei numeri costruibili contiene solo numeri che si possono ottenere a partire dai numeri razionali facendo un numero finito di somme, sottrazioni, moltiplicazioni, divisioni e radici quadrate”.
“Non si può fare di meglio, vero?”.
“No, il compasso ti permette di estrarre soltanto radici quadrate. Naturalmente puoi fare radici di radici, ottenere radici quarte, radici ottave, e così via. Non potrai mai ottenere radici cubiche, ad esempio”.
“E pi greco?”.
“Pi greco è stato un grossissimo problema”.
“Addirittura”.
“Eh sì. Abbiamo già raccontato un po' della sua storia: all'inizio non si sapeva nemmeno se fosse un numero razionale oppure no”.
“Ci aveva lavorato anche Archimede, vero?”.
“Giusto, lui ha studiato poligoni fino a 96 lati”.
“Roba da matti”.
“C'è di peggio, Ludolph van Ceulen è arrivato a poligoni con 230 lati”.
“Santo cielo”.
“Ma nessuno, fino al 1761, è riuscito a scoprire se pi greco fosse razionale o irrazionale”.
“E che è successo nel 1761?”.
“Lambert, utilizzando concetti di analisi, arriva a dimostrare l'irrazionalità”.
“L'analisi?”.
“Sì, un teorema di teoria dei numeri dimostrato con l'analisi. Abbastanza inaudito: in teoria dei numeri si dimostrano cose molto complicate, eppure senza l'analisi non si riesce a studiare pi greco”.
“Che roba”.
“Eppure nemmeno questa dimostrazione era sufficiente per dimostrare l'impossibilità di quadrare il cerchio”.
“Ah, già, con riga e compasso si possono costruire numeri irrazionali, dato che si possono fare tutte le radici quadrate che si vuole”.
“Esatto. Bisogna dimostrare qualcosa di più”.
“E qualcuno c'è riuscito”.
“Sì, nel 1882 c'è riuscito Lindemann, dimostrando che pi greco è addirittura trascendente”.
“Trascendente?”.
“Sì. Significa che non può essere soluzione di nessuna equazione polinomiale a coefficienti interi”.
“Non capisco”.
“Allora, partiamo dall'inizio. I numeri naturali sono soluzioni di equazioni polinomiali di primo grado”.
“Continuo a non capire”.
“Per esempio, il numero 42”.
“E di quale equazione è soluzione?”.
“x − 42 = 0”.
“Ah, ma certo”.
“Ma anche tutte le frazioni sono soluzioni di equazioni polinomiali di primo grado”.
“Mh, per esempio?”.
“Per esempio, 2/3 è soluzione dell'equazione 3x − 2 = 0”.
“Già, era ovvio anche questo”.
“Le radici quadrate sono invece soluzioni di equazioni di secondo grado. Per esempio, la radice di 2 è una delle soluzioni di x2 − 2 = 0”.
“Ok, sto capendo. Più aumenti il grado, più complicate sono le soluzioni”.
“Esatto. Esistono però alcuni numeri irrazionali che non possono essere soluzioni di nessuna equazione polinomiale, qualunque grado essa abbia”.
“Ma pensa. E pi greco è uno di questi numeri? Ce ne saranno pochi, suppongo”.
“Supponi male, in realtà i numeri irrazionali sono quasi tutti trascendenti”.
“Eh, ma com'è possibile?”.
“Beh, forse ricordi la differenza tra insieme infinito numerabile e insieme infinito non numerabile”.
“Qualcosa ricordo”.
“In sostanza, l'infinito numerabile è quello dei numeri naturali. Puoi contare, metti un numero dopo l'altro, e via così. Anche i numeri interi e i numeri razionali sono un'infinità numerabile: si possono mettere in fila e li si possono contare, mettendoli in corrispondenza biunivoca con i numeri naturali”.
“I numeri reali invece no”.
“No, loro no, sono molti di più. Abbiamo dimostrato che è impossibile metterli in corrispondenza biunivoca con i numeri naturali”.
“E i numeri trascendenti?”.
“Allora, facciamo ordine. Tutti i numeri reali che non sono razionali si dicono irrazionali, ma questa divisione è ancora grossolana. I numeri costruibili con riga e compasso sono solo una parte degli irrazionali. Una piccola parte”.
“Piccola?”.
“Sì, sono ancora un'infinità numerabile. Ma addirittura tutti i numeri che sono soluzioni di equazioni polinomiali sono una piccola parte degli irrazionali”.
“Ma dai”.
“Sì, questi numeri si chiamano numeri algebrici”.
“Santo cielo, ma quante categorie ci sono?”.
“Eh, un po'. Ma lasciami spiegare perché i numeri algebrici sono pochi. Sai che un'equazione polinomiale ha, al massimo, tante soluzioni quanto è il suo grado”.
“Sì”.
“Quante equazioni polinomiali esistono?”.
“Infinite, naturalmente”.
“Certo, ma formano un'infinità numerabile o non numerabile?”.
“Non ne ho idea”.
“Beh, un'equazione polinomiale è identificata dai suoi coefficienti”.
“Sì, ci sarà un termine noto, un coefficiente del termine di primo grado, un coefficiente del termine di secondo grado, e così via”.
“Ottimo. Come vedi, stai contando i coefficienti”.
“Ah”.
“Li stai mettendo in corrispondenza biunivoca con i numeri naturali”.
“Già”.
“E quindi questi coefficienti costituiscono un'infinità numerabile. E allora anche tutte le equazioni polinomiali sono un'infinità numerabile, e così le loro soluzioni, che chiamiamo numeri algebrici”.
“Gulp”.
“Quindi i numeri irrazionali non algebrici, che vengono chiamati trascendenti, sono molti di più. Infinitamente di più”.
“Mamma mia. Comincio a pensare che la dimostrazione del fatto che pi greco è trascendente non sia proprio semplice semplice”.
“Pensi bene: se la dimostrazione è del 1882 significa che è difficile”.
“E non è che ora me la vuoi spiegare nel dettaglio, vero?”.
“No, è troppo difficile, bisogna mettersi d'impegno e studiarla in dettaglio. Col rischio di non capirne il senso, se non si cerca prima di avere un'idea di quello che si sta facendo. Bisogna capire, prima, qualche proprietà di questi numeri trascendenti, che non sappiamo nemmeno nominare”.
“In che senso?”.
“Beh, noi possiamo dare nomi solo a un'infinità numerabile di numeri”.
“Cosa?”.
“Esiste un numero finito di lettere dell'alfabeto. Con quelle puoi fare infinite parole, ma sono certamente un'infinità numerabile: puoi fare un gigantesco dizionario e mettere tutto in fila”.
“Come la biblioteca di Babele!”.
“Quasi. La biblioteca di Babele, pur enorme, contiene un numero finito di libri. Ogni libro ha 410 pagine, e pur considerando tutte le permutazioni di caratteri che esse possono contenere, si arriverà a un certo punto alla fine. Le parole che invece potremmo usare per definire i nostri numeri non hanno nessuna limitazione, e quindi potremmo costruirne un'infinità. Solo numerabile, però”.
“Quindi esistono numeri che non solo non potremo mai conoscere, ma che non potremo nemmeno chiamare per nome, come invece facciamo con pi greco?”.
“Ne esistono tantissimi, sì. Più delle parole che potremo mai inventare”.
“Mi gira la testa”.
“Capisco. Ma un po' ci vengono in aiuto le care frazioni: ogni numero irrazionale può essere approssimato, bene quanto si vuole, con delle frazioni”.
“Che è quello che facciamo in realtà quando facciamo calcoli con i numeri irrazionali, vero?”.
“Esatto: nessuna calcolatrice e nessun computer ha infinita memoria per poter contenere le infinite cifre di un numero irrazionale. Però i numeri algebrici e i numeri trascendenti si comportano in modi un po' diversi quando cerchiamo di approssimarli con le frazioni”.
“In che senso?”.
“Nel senso che i numeri algebrici possiamo approssimarli bene quanto vogliamo, ma non troppo”.
“Eh?”.
“Immagina di approssimare pi greco con delle frazioni: come puoi fare?”.
“Potrei scrivere 3/1, 31/10, 314/100, 3141/1000, e così via”.
“Giusto. Non è detto che questo sia il miglior modo di procedere, ma rende l'idea: se vuoi migliorare l'approssimazione, devi usare numeratori e denominatori sempre più grandi”.
“Certo, se voglio produrre più cifre decimali, mi sembra ovvio che devo aggiungere zeri al denominatore: è la notazione scientifica”.
“Ti sembra ovvio, ed è un bene, tieni presente però che la scelta di mettere al denominatore una potenza di 10 potrebbe non essere la scelta migliore. Si potrebbe fare meglio, insomma”.
“Ma cosa significa fare meglio di una approssimazione con un grado di precisione alto quanto vogliamo?”.
“Significa che, a parità di numero di cifre di numeratore e denominatore, esistono frazioni che approssimano pi greco meglio delle tue. Per esempio, Archimede, con i suoi poligoni di 96 lati, è arrivato a approssimare pi greco con le due frazioni 223/71 e 22/7, la prima per difetto e la seconda per eccesso”.
“Fammi fare i conti: 223/71 fa 3.1408 e 22/7 fa 3.1429. Le prime due cifre dopo la virgola sono esatte”.
“Mentre la tua frazione con due cifre al denominatore è 31/10 che approssima bene solo la prima cifra dopo la virgola”.
“Ah, ecco cosa intendevi. Io per approssimare bene anche la seconda cifra devo scrivere 314/100”.
“Pensa che con denominatori di tre cifre si possono approssimare bene le prime sei cifre dopo la virgola”.
“Cosa?”.
“Eh, sì. La frazione 355/113 è uguale a 3.14159204, le prime sei cifre dopo la virgola sono corrette”.
“Ma tu guarda. Bellina questa frazione”.
“Pensa che ha anche un nome: si chiama Milü, una parola cinese che significa più o meno frazione che approssima bene”.
“Eh eh, mi piace. Ma come mai cinese?”.
“Perché fu coniata dal matematico e astronomo cinese Zu Chongzhi nella seconda metà del quattrocento”.
“Ah, immagino quindi che abbia scoperto questa approssimazione più o meno quando l'hanno scoperta i matematici europei”.
“No, no, hai capito male. Parlo proprio del quattrocento, non del millequattrocento. Questo signore ha dato ai cinesi un'approssimazione straordinaria di pi greco mille anni prima che fosse conosciuta in Europa”.
“Gulp”.
“Quindi, per tornare alle buone approssimazioni dei numeri irrazionali: fissato un denominatore, come sono fatte le frazioni che meglio approssimano un numero irrazionale? Quanto bene si può approssimare un certo numero con una frazione che al denominatore ha due cifre? Tre cifre? n cifre?”.
“Ah, ecco cosa intendevi”.
“Già. Ecco una tabella delle migliori frazioni che approssimano pi greco, con, a fianco, l'errore”.
22/7 3.142857142857 0.00126448926735 355/113 3.141592920353 2.66764189405e-07 312689/99532 3.141592653618 2.91433543964e-11 146408/364913 3.141592653591 1.61071156413e-12 5419351/1725033 3.141592653589 2.22044604925e-14
“Ah, ecco 22/7 e 355/113. Come mai non hai elencato frazioni con quattro cifre al denominatore?”.
“Perché nessuna di loro approssima meglio pi greco di quanto non faccia 355/113.”.
“Ma tu guarda, non sapevo queste cose”.
“Ora ti mostro le migliori approssimazioni per radice di 2:”.
7/5 1.400000000000 0.0142135623731 99/70 1.414285714285 7.21519126192e-05 1393/985 1.414213197969 3.64403552e-07 8119/5741 1.414213551646 1.07270403671e-08 114243/80782 1.414213562427 5.41782174679e-11 665857/470832 1.414213562374 1.59472435257e-12 9369319/6625109 1.414213562373 8.21565038223e-15
“Compaiono denominatori di tutte le lunghezze, da 1 a 7”.
“Sì, anche se da un paio di esempi non si possono estrarre regole”.
“Ah, certo”.
“Però c'è qualcosa che si può dire, su queste approssimazioni”.
“Che cosa?”.
“Che i numeri algebrici rispettano certe regole, i trascendenti no”.
“Già, loro trascendono”.
1 commento:
ma-che-bello!
Questi articoli, per usare sempre le parole del Sommo, sono soddisfacenti in modo che "intender non può chi non lo prova"
Posta un commento