Già i Pitagorici avevano scoperto che la diagonale di un quadrato è un numero incommensurabile con il lato del quadrato stesso. In termini moderni, questo significa che radice di 2 non è un numero razionale. Però si può costruire con riga e compasso: in effetti, abbiamo visto che ogni radice quadrata può essere costruita con riga e compasso.
«Vorrà dire che con riga e compasso si possono costruire tutti i numeri reali, e non solo i razionali, no?».
«Eh, no, non è così. È per questo motivo che i greci non sono riusciti a risolvere alcuni problemi, come ti avevo detto».
«Ah. Ma allora quali sono i numeri reali che non si riescono a costruire?».
«Eh, per rispondere a questa domanda dobbiamo tornare a parlare di algebra. Abbiamo detto che con le quattro operazioni possiamo costruire il campo dei numeri razionali».
«Vero».
«Chiamiamolo F0».
«Mmmmh, come mi piace poco quell'indice…».
«F sta per field, mentre 0 sta a significare che poi ne faremo altri».
«Lo immaginavo».
«Allora, prendiamo un numero che non appartiene a F0, per esempio la famosa radice di 2, e aggiungiamola all'insieme».
«Possiamo?».
«Certo che possiamo, i matematici possono fare tutto. Bisogna vedere se quello che fanno ha senso, ma questo è un altro discorso».
«Volevo dire: il nuovo insieme che otteniamo ha le proprietà di quello vecchio? È un campo?».
«Tu cosa dici?».
«Boh, non so, posso provare a guardarci. Ah, ma no, certo che no, mi basta fare una somma semplice: 1+√2 non sta in quell'insieme».
«Che, quindi, non è più un campo, perfetto. Ora, quanta roba dobbiamo aggiungere a F0, oltre a √2, perché il nuovo insieme che otteniamo sia di nuovo un campo?».
«Uh, domanda difficile, vediamo. Se devo poter fare tutte le somme, l'insieme deve contenere numeri del tipo a+√2».
«Giusto. Ma se vuoi fare √2+√2?».
«Ah, quello fa 2√2. Ok, ci sono, l'insieme deve contenere numeri del tipo a+b√2».
«Bene, e così hai messo a posto le somme».
«Ok. Se voglio fare anche delle sottrazioni, bé, mi pare che non ci siano problemi, non devo aggiungere nient'altro».
«Esatto: la differenza tra a+b√2 e c+d√2 è ancora un numero del tipo A+B√2, quindi siamo a posto. Per quanto riguarda la moltiplicazione, invece?».
«Ah, ormai ho capito il trucco: provo a moltiplicare due numeri del tipo A+B√2 e guardo se il risultato è ancora di quel tipo lì oppure no».
«Prova».
«Subito. Allora, ecco qua: (a+b√2) + (c+d√2) dà come risultato (a+c) + (b+d)√2, che è ancora un numero del tipo A+B√2».
«Bene. Vediamo la divisione, adesso?».
«Subito. Ecco: (a+b√2) diviso (c+d√2) fa… uhm, non lo so mica quanto fa».
«Perché?».
«Eh, perché non la so fare la divisione con una radice».
«Sì, bé, in un certo senso nessuno la sa fare».
«Eh?».
«Sì, per dare un senso a una divisione del genere, i Veri Matematici usano un trucchetto che si chiama razionalizzazione del denominatore».
«Uh, mi pare di ricordare qualcosa dai miei studi di algebra».
«Bene. Ti ricordi come si fa?».
«Non tanto, mi pare che si dovesse moltiplicare la frazione, sia al numeratore che al denominatore, per una certa espressione, in modo da eliminare la radice di due al denominatore? Era una cosa del genere?».
«Esatto. Ti faccio vedere i passaggi:».
«Bello! Quindi anche con la divisione siamo a posto».
«Già, la divisione di due numeri del tipo A+B√2 produce un risultato dello stesso tipo».
«E quindi abbiamo ottenuto il nostro nuovo campo».
«Che, indovina un po', chiameremo F1».
«Mh».
«Ci sarebbe da aggiungere una considerazione: quando si fa la divisione, si ottiene un denominatore».
«Sì, è c2-2d2».
«Ecco, bisogna che quel denominatore non diventi mai zero».
«Ah. Potrebbe diventarlo?».
«No, dato che stiamo lavorando con numeri razionali: se quel denominatore fosse uguale a zero, la radice di 2 dovrebbe essere un numero razionale».
«Cosa che non è vera».
«Infatti, e quindi siamo a posto. Ti faccio notare anche che il nuovo campo F1 poteva essere costruito a partire da un qualunque numero irrazionale, radice di 2 non ha niente di speciale».
«Sì, giusto, se al posto di √2 usiamo √3 non cambia nulla, si possono ripetere gli stessi calcoli».
«Esatto. E se invece usiamo √4, potremmo avere dei valori di c e d che annullano il denominatore. Quindi, riassumendo ecco quello che abbiamo fatto: abbiamo preso il campo dei numeri razionali, abbiamo preso un elemento k tale che √k non è razionale, e abbiamo ampliato il campo costruendo tutti i numeri del tipo A+B√k, con A e B razionali».
«E questo è F1».
«E poi ci saranno F2, F3, e così via».
«Grrr».
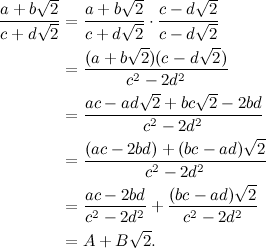
Nessun commento:
Posta un commento