Se noi ci mettiamo sul piano cartesiano, possiamo anche scrivere le equazioni delle trasformazioni geometriche. Per esempio, se si indica il vettore v di una traslazione mediante le sue componenti lungo gli assi cartesiani (e cioè v=(a,b)), allora l'equazione della traslazione di vettore v può essere scritta semplicemente in questo modo:
T(x,y) = (x+a,y+b).
Ora complichiamo le cose semplici. Gli studenti universitari imparano presto che ciò che i professori chiamano geometria è in realtà algebra lineare, almeno per qualche mese. Quella scritta sopra è, in effetti, una trasformazione lineare. Bene, ad ogni trasformazione lineare è associata una matrice, oggetto scomodo e dalle proprietà misteriose. In forma matriciale la semplice equazione scritta sopra diventa così:
Il fatto che il punto di coordinate (x,y) sia diventato (x,y,1) è dovuto a due considerazioni. La prima è che così l'operazione con le matrici funziona, altrimenti non si riuscirebbe a ottenere come risultato (x+a,y+b). La seconda la facciamo più avanti.
Diciamo dunque che la matrice associata alla traslazione di vettore v(a,b) è la seguente:
Quindi lo studio delle proprietà delle traslazioni potrebbe essere fatto analizzando questo tipo di matrici (ma noi non lo facciamo). E anche il gruppo delle traslazioni diventa il gruppo delle matrici di questo tipo, mentre la composizione di traslazioni diventa la moltiplicazione righe per colonne delle matrici.
Ma lasciamo queste cose agli studenti universitari di geometria, e passiamo ad altre trasformazioni.
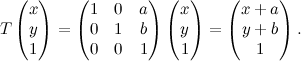
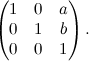
Nessun commento:
Posta un commento